No antigo Egito por volta do ano 3000 a.C., o faraó Sesóstris distribuiu algumas terras às margens do Rio Nilo para alguns agricultores privilegiados. O privilégio em possuir essas terras era porque todo ano, no mês de julho, as águas do rio inundavam essa região ao longo de suas margens e fertilizavam os campos. Essas terras, portanto, eram bastante valorizadas.
Porém, era necessário remarcar os terrenos de cada agricultor em setembro, quando as águas baixavam. Os responsáveis por essa marcação eram os agrimensores, que também eram chamados de estiradores de corda, pois mediam os terrenos com cordas nas quais uma unidade de medida estava marcada.
Essas cordas eram esticadas e se verificava quantas vezes a tal unidade de medida cabia no terreno, mas nem sempre essa medida cabia inteira nos lados do terreno. Esse problema só foi resolvido quando os egípcios criaram um novo número: o número fracionário. Ele era representado com o uso de frações, porém os egípcios só entendiam a fração como uma unidade (ou seja, frações cujo numerador é igual a 1).
Eles escreviam essas frações com uma espécie de sinal oval escrito em cima do denominador. Mas os cálculos eram complicados, pois no sistema de numeração que usavam no antigo Egito os símbolos se repetiam muitas vezes.[1]
Só ficou mais fácil trabalhar com as frações quando os hindus criaram o Sistema de numeração decimal, quando elas passaram a ser representadas pela razão de dois números naturais.
Desde então, as frações foram usadas para a resolução de diversos tipos de problemas matemáticos. Uma das formas mais correntes de se trabalhar com frações é a porcentagem, em que se expressa uma proporção ou uma relação a partir de uma fração cujo denominador é 100. O uso de frações também é de valia extrema para a resolução de problemas que envolvem regra de três.
De modo simples, pode-se dizer que uma fração de um número, representada de modo genérico como  designa o inteiro dividido em
designa o inteiro dividido em 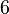 partes iguais ao qual usa-se o número
partes iguais ao qual usa-se o número 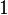 de partes.[2] Neste caso,
de partes.[2] Neste caso,  corresponde ao numerador, enquanto
corresponde ao numerador, enquanto  corresponde ao denominador, que não pode ser igual a zero.[2] [3]
corresponde ao denominador, que não pode ser igual a zero.[2] [3]
 designa o inteiro dividido em
designa o inteiro dividido em 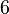 partes iguais ao qual usa-se o número
partes iguais ao qual usa-se o número 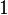 de partes.[2] Neste caso,
de partes.[2] Neste caso,  corresponde ao numerador, enquanto
corresponde ao numerador, enquanto  corresponde ao denominador, que não pode ser igual a zero.[2] [3]
corresponde ao denominador, que não pode ser igual a zero.[2] [3]
O denominador corresponde ao número de partes que um todo será dividido e o numerador corresponde ao número de partes que serão consideradas.
Ex.: Uma professora tem que dividir três folhas de papel de seda entre quatro alunos, como ela pode fazer isso?
Cada aluno ficara com 3:4 =  (lê-se três-quartos) da folha. Ou seja, você vai dividir cada folha em 4 partes e distribuir 3 para cada aluno.
(lê-se três-quartos) da folha. Ou seja, você vai dividir cada folha em 4 partes e distribuir 3 para cada aluno.
 (lê-se três-quartos) da folha. Ou seja, você vai dividir cada folha em 4 partes e distribuir 3 para cada aluno.
(lê-se três-quartos) da folha. Ou seja, você vai dividir cada folha em 4 partes e distribuir 3 para cada aluno.
Por exemplo, a fração 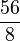 (lê-se cinquenta e seis-oitavos) designa o quociente de 56 por 8. Ela é igual a 7, pois 7 × 8 = 56. A divisão é, note-se, a operação inversa da multiplicação.
(lê-se cinquenta e seis-oitavos) designa o quociente de 56 por 8. Ela é igual a 7, pois 7 × 8 = 56. A divisão é, note-se, a operação inversa da multiplicação.
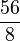 (lê-se cinquenta e seis-oitavos) designa o quociente de 56 por 8. Ela é igual a 7, pois 7 × 8 = 56. A divisão é, note-se, a operação inversa da multiplicação.
(lê-se cinquenta e seis-oitavos) designa o quociente de 56 por 8. Ela é igual a 7, pois 7 × 8 = 56. A divisão é, note-se, a operação inversa da multiplicação.
Os números expressos em frações são chamados de números racionais, cujo conjunto é representado por 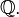 Assim, o conjunto dos números racionais podem ser escritos na forma
Assim, o conjunto dos números racionais podem ser escritos na forma 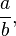 sendo
sendo 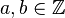 e
e  o que resulta em:
o que resulta em: 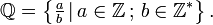 [4] [5]
[4] [5]
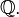 Assim, o conjunto dos números racionais podem ser escritos na forma
Assim, o conjunto dos números racionais podem ser escritos na forma 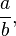 sendo
sendo 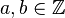 e
e  o que resulta em:
o que resulta em: 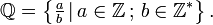 [4] [5]
[4] [5]
Outro modo de enxergar frações é imaginar uma linha reta entre os números 0 e 1. As frações serão pontos nessa reta. Por exemplo, a fração 1/2 é representada por um ponto exatamente na metade dessa reta.,
É possível efetuar operações básicas com as frações: adição, subtração, multiplicação, divisão, potenciação, radiciação
Tipos de frações
- Própria: o numerador é menor que o denominador. Ex.:
 (lê-se um-meio).
(lê-se um-meio). - Imprópria: o numerador é maior ou igual ao denominador.[2] Ex.:
 (lê-se nove-quintos).
(lê-se nove-quintos). - Mista: constituída por uma parte inteira e uma fracionária.[6] Ex.:
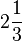 (lê-se dois um-terço). Pode-se encontrar uma fração imprópria a partir do número misto:
(lê-se dois um-terço). Pode-se encontrar uma fração imprópria a partir do número misto: 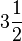 (lê-se três um-meio) => 2x3=6; 6+1=7 (7=numerador/2=denominador), e assim por diante, repetindo o denominador.
(lê-se três um-meio) => 2x3=6; 6+1=7 (7=numerador/2=denominador), e assim por diante, repetindo o denominador. - Aparente: é quando o numerador é múltiplo ao denominador, ou seja um número inteiro escrito em forma de fração. Ex.:
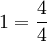 (lê-se um igual a quatro-quartos).
(lê-se um igual a quatro-quartos). - Equivalentes: aquelas que mantêm a mesma proporção de outra fração. Ex.:

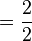 (lê-se quatro-quartos igual a dois-meios) ou
(lê-se quatro-quartos igual a dois-meios) ou 
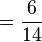 (lê-se três-sétimos igual a seis-quatorze avos). Veja que as frações se relacionam por um fator multiplicativo: no primeiro caso,
(lê-se três-sétimos igual a seis-quatorze avos). Veja que as frações se relacionam por um fator multiplicativo: no primeiro caso,  é 2 vezes
é 2 vezes  e no segundo caso
e no segundo caso 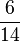 é 2 vezes
é 2 vezes  .
. - Irredutível: o numerador e o denominador são primos entre si, não permitindo simplificação. Ex.:
 (lê-se nove-vinte e dois avos).
(lê-se nove-vinte e dois avos). - Unitária: o numerador é igual a 1 e o denominador é um inteiro positivo. Ex.:

- Egípcia: fração que é a soma de frações unitárias, distintas entre si. Ex:
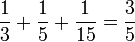 (lê-se um-terço mais um-quinto mais um-quinze avos igual a três-quintos).
(lê-se um-terço mais um-quinto mais um-quinze avos igual a três-quintos). - Decimal: o denominador é uma potência de 10(100,1000,10000…). Ex.:
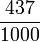 (lê-se quatrocentos e trinta e sete-mil avos).
(lê-se quatrocentos e trinta e sete-mil avos). - Composta: fração cujo numerador e denominador são frações:
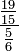 (lê-se dezenove-quinze avos por cinco-sextos).
(lê-se dezenove-quinze avos por cinco-sextos). - Contínua: fração constituída a partir de uma sequência de inteiros naturais
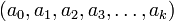 da seguinte maneira
da seguinte maneira 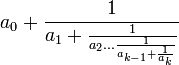
- Algébrica: fração onde no denominador, há incógnita
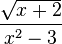 .
.
Fonte:Wikipédia.
muito bom valeu <3
ResponderExcluiruepa..mt bommmm serio recomendo
ResponderExcluir