Que tal um desafio? Pense no menor número que puder!Será que você pensou no zero? Se sim, preciso lhe contar que há alguns números que conseguem ser menores que ele. Alguns não,existem infinitos números menores que o zero! E é bem provável que você já os tenha visto por aí.
Sempre que estamos no inverno as temperaturas caem. Algumas cidades do Sul do Brasil chegam até mesmo a nevar. Quando isso acontece, a temperatura está menor do que zero. Em Urupema, cidade de Santa Catarina, a temperatura já chegou a atingir-6,8°C no ano de 2013.
Vou propôr-lhe um novo desafio! Dessa vez será uma perguntinha rápida: “Você tem R$ 5,00 reais em sua carteira, perde uma aposta para seu amigo e fica devendo R$ 8,00 para ele. Após pagar a aposta, qual será sua situação?” Nesse caso, se você pagar os R$ 5,00 reais ao seu amigo, ainda ficará devendo R$ 3,00 a ele. Podemos dizer que seu saldo é de – 3 reais.
Os números negativos que citamos, assim como todos os outros existentes, pertencem a um conjunto numérico muito especial chamado Conjunto dos Números Inteiros, que pode ser representado pela letra  . Os números inteiros são formados pelos números naturais e também pelos números negativos, além do zero, que não possui sinal. Podemos representar esse conjunto numérico da seguinte forma:
. Os números inteiros são formados pelos números naturais e também pelos números negativos, além do zero, que não possui sinal. Podemos representar esse conjunto numérico da seguinte forma:
 = {…, – 3, – 2, – 1, 0, 1, 2, 3, …}.
= {…, – 3, – 2, – 1, 0, 1, 2, 3, …}.
Esse conjunto é dito infinito positivamente e infinito negativamente, pois possui infinitos números positivos e negativos. Outra forma de visualizar os números negativos é através da reta numérica, pois ela consegue organizá-los de forma eficiente, além do fato de que a reta dá-nos a ideia de infinidade. Na reta numérica, à direita do zero, ficam os números naturais (positivos) e, à esquerda do zero, ficam os números negativos:
.jpg)
Representando os números inteiros através da reta numérica
Há algumas situações em que não é adequado utilizar todos os números inteiros. Para esses casos, temos alguns conjuntos numéricos especiais e suas representações:
Conjunto dos Números Inteiros não nulos (sem o zero)
 * = {…, – 3, – 2, – 1, 1, 2, 3, …}.
* = {…, – 3, – 2, – 1, 1, 2, 3, …}.
Conjunto dos Números Inteiros não negativos (zero e números positivos)
 + = {0, 1, 2, 3, …}.
+ = {0, 1, 2, 3, …}.
Conjunto dos Números Inteiros positivos (apenas números maiores que zero)
 *+ = { 1, 2, 3, …}.
*+ = { 1, 2, 3, …}.
Conjunto dos Números Inteiros não positivos (zero e números negativos)
 – = {…, – 3, – 2, – 1, 0}.
– = {…, – 3, – 2, – 1, 0}.
Conjunto dos Números Inteiros negativos (apenas números menores que o zero)
 *– = {…, – 3, – 2, – 1}.
*– = {…, – 3, – 2, – 1}.


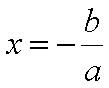
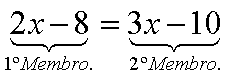
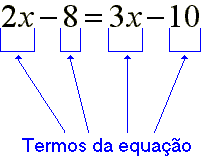
 .
. é um número racional, sendo que p e qsão números inteiros e q ≠ 0. Observe que
é um número racional, sendo que p e qsão números inteiros e q ≠ 0. Observe que 
 ) e o conjunto do
) e o conjunto do ) pertencem ao conjunto dos números racionais (
) pertencem ao conjunto dos números racionais ( , se dividirmos seu numerador
, se dividirmos seu numerador .jpg)
 designa o inteiro
designa o inteiro 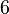 partes iguais ao qual usa-se o número
partes iguais ao qual usa-se o número 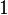 de partes.
de partes. corresponde ao
corresponde ao  corresponde ao
corresponde ao  (lê-se três-quartos) da folha. Ou seja, você vai dividir cada folha em 4 partes e distribuir 3 para cada aluno.
(lê-se três-quartos) da folha. Ou seja, você vai dividir cada folha em 4 partes e distribuir 3 para cada aluno.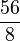 (lê-se cinquenta e seis-oitavos) designa o quociente de 56 por 8. Ela é igual a 7, pois 7 × 8 = 56. A divisão é, note-se, a operação inversa da
(lê-se cinquenta e seis-oitavos) designa o quociente de 56 por 8. Ela é igual a 7, pois 7 × 8 = 56. A divisão é, note-se, a operação inversa da 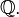 Assim, o conjunto dos
Assim, o conjunto dos 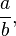 sendo
sendo 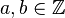 e
e  o que resulta em:
o que resulta em: 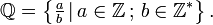
 (lê-se um-meio).
(lê-se um-meio). (lê-se nove-quintos).
(lê-se nove-quintos).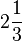 (lê-se dois um-terço). Pode-se encontrar uma fração imprópria a partir do número misto:
(lê-se dois um-terço). Pode-se encontrar uma fração imprópria a partir do número misto: 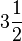 (lê-se três um-meio) => 2x3=6; 6+1=7 (7=numerador/2=denominador), e assim por diante, repetindo o denominador.
(lê-se três um-meio) => 2x3=6; 6+1=7 (7=numerador/2=denominador), e assim por diante, repetindo o denominador.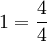 (lê-se um igual a quatro-quartos).
(lê-se um igual a quatro-quartos).
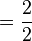 (lê-se quatro-quartos igual a dois-meios) ou
(lê-se quatro-quartos igual a dois-meios) ou 
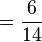 (lê-se três-sétimos igual a seis-quatorze avos). Veja que as frações se relacionam por um fator multiplicativo: no primeiro caso,
(lê-se três-sétimos igual a seis-quatorze avos). Veja que as frações se relacionam por um fator multiplicativo: no primeiro caso,  e no segundo caso
e no segundo caso 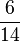 é 2 vezes
é 2 vezes  (lê-se nove-vinte e dois avos).
(lê-se nove-vinte e dois avos).
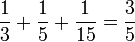 (lê-se um-terço mais um-quinto mais um-quinze avos igual a três-quintos).
(lê-se um-terço mais um-quinto mais um-quinze avos igual a três-quintos).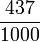 (lê-se quatrocentos e trinta e sete-mil avos).
(lê-se quatrocentos e trinta e sete-mil avos).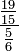 (lê-se dezenove-quinze avos por cinco-sextos).
(lê-se dezenove-quinze avos por cinco-sextos).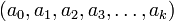 da seguinte maneira
da seguinte maneira 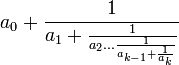
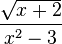 .
.